Расчет характеристик динамики движения самолета в вихревом следе

Для расчета характеристик движения летательного аппарата (ЛА) под действием сил и моментов от воздействия вихревого следа запишем систему уравнений динамики движения твердого тела в связанной системе координат. Будем считать, что масса и моменты инерции ЛА на рассматриваемых интервалах времени неизменны и соответствуют исходным. При условии, что оси связанной системы координат сов­падают с главными осями инерции ЛА, система уравнений движения центра масс ЛА имеет следующий вид:

m(d — + ttyК — ttzVy) = X + Px — G sin 0;

m(d — + fizVx — QxVz) = Y + Py — G cos 0 cos 7; (8.7)

m (+ QxVy — QyVxJ = Z + Pz + Gcos 0 sin 7,

где Vx, Vy, Vz — проекции вектора скорости Vk; Qx, Qy, Qz — проекции вектора угловой скорости Q; X, Y, Z — проекции аэродинамической силы RtextA (t); Px, Py, Pz — проекции тяги двигателя P (t).

При принятых допущениях угловое движение ЛА описывается уравнениями Эйлера:

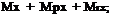
Ix dt — + (Iz — Iy ) Qy Qz

где Ix, Iy, Iz — моменты инерции ЛА относительно осей связанной системы координат; Mx, My, Mz, MPx, MPy, MPz, MPx, MPy, MPz —

проекции моментов M (t), Mp (t) и Mp (t).

Система уравнений (8.7) и (8.8) позволяет найти проекции посту­пательной и угловой скоростей. Для определения координат центра тяжести ЛА и положения связанной системы координат относительно
неподвижной необходимо использовать шесть кинематических диффе­ренциальных уравнений:

Qy sin y + Q. z cos y;

Q. x — tg§ (Qy cos y — Qz sin y);

fiy cos y — sin y.

cos 6

Vx cos § cos ф + Vy (sin y sin ф — cos y cos ф sin §) + (8.9)

+ Vz (cos y sin ф + sin § sin y cos ф)

Vx sin § + Vy cos y cos § — Vz sin y cos §;

— Vx cos § sin ф + Vy (sin y cos ф + cos y sin § sin ф) +

+ Vz (cos y cos ф — sin y sin § sin ф).

Системы уравнений (8.7)-(8.9) при заданных начальных условиях од­нозначно определяют движение летательных аппаратов. Однако для решения системы уравнений (8.7) и (8.8) необходимо в каждый момент времени знать величины аэродинамической силы Ra (t) и момента M (t), действующих на ЛА (при этом считаем, что все остальные вели­чины P (t), Mр (t) и Mp (t) известны). Таким образом, для решения системы уравнений (8.7)-(8.9) в каждый момент времени будем опре­делять аэродинамическую силу Ra (t) и аэродинамический момент M (t), действующие на ЛА, по методу, описанному в разд. 8.2.

При необходимости можно учесть и работу летчика. Углы откло­нения органов управления определяются законами управления ЛА, динамическими свойствами систем управления и летчика. Для моде­лирования системы управления ЛА введем следующие допущения:

— проводка управления абсолютно жесткая;

— распределенные массы и жєсткости проводки управления заме­ним сосредоточенными;

— люфты и силы сухого трения в проводке отсутствуют;

— силы вязкого трения будем считать пропорциональными скорости отклонения ручки управления самолетом (РУС) и руля;

— жесткость загрузочного механизма постоянна.

При указанных допущениях в области рабочих частот от летчика f = 1 — 3 Гц звенья системы управления можно считать усилительны­ми. Тогда передаточная функция системы управления будет иметь вид

K

WCy = K, (8.10)

где К — передаточное число проводки управления от РУС к рулю; C — жесткость загрузки РУС.

Лєтчик являєтся наиболее сложным звєном в контуре управле­ния, Его свойства изменяются в широких пределах и в зависимости от состояния могут быть различными, т. е, на них влияет множество факторов, Однако можно выделить следующие общие свойства,

— Летчик формирует управляющие воздействия в зависимости от величины и направления внешнего возмущения или в зависи­мости от величины сигнала рассогласования,

— Ответная реакция летчика на внешнее возмущение наступает не сразу, а с некоторым запаздыванием, которое зависит от на­правления и интенсивности возмущения, от количества парамет­ров, контролируемых летчиком и от его психофизиологического состояния, На интенсивные акселерационные воздействия летчик реагирует рефлекторно, с запаздыванием 0,13—0,6 с,

— Летчик имеет зону нечувствительности, Если интенсивность раз­дражителя ниже порога чувствительности, летчик не реагирует на него,

— Зная о своем запаздывании, летчик стремится компенсировать его упреждением,

Единой модели действий летчика для всех случаев не существует. Для каждой конкретной задачи разрабатываются свои дискретные или непрерывные модели действий летчика, Для управления или стаби­лизации какого-либо одного параметра xi установлен следующий вид передаточной функции летчика:

где Дхі = xi — хізіщ ; K = A. P/Axi — коэффициент усиления летчика; т = 0,13—0,3 с — запаздывание летчика; 1/T^P + 1 — инерционность летчика по приему и распознаванию информации, Тл2 ^ 2 с; 1/ТлзР + 1 — нервно-мускульное запаздывание летчика, Тл3 = 0,1 — 0,3 с; ТлiP + 1 — способность летчика работать с упрежде­нием, Тл 1 ^ 2,5 с,

Таким образом, нелинейная математическая модель динамики про­странственного движения ЛА с учетом управляющих воздействий опи­сывается в общем случае системой уравнений (8,7)—(8,11), Как видно из этих уравнений, существует сложная взаимосвязь входящих в них параметров, Так, движение летательных аппаратов зависит от действу­ющей на них аэродинамической нагрузки, В свою очередь величина аэродинамических сил и моментов зависит от характера движения ЛА, В процессе движения изменяется положение рулевых поверхностей, что также влияет на аэродинамические характеристики ЛА и характер его перемещения, Следовательно, необходимо совместное решение уравне­ний динамики движения, нелинейной нестационарной аэродинамики и уравнений, описывающих функционирование контура управления, Практически это осуществляется последовательным решением этих уравнений шаг за шагом по времени,

t = 4,5 c

t = 5,5 c

t = 6 c

21 м

60 м

Рис. 8.25. Траектория движения самолета Як-40 в вихревом следе самолета Ил-76, полученная расчетом. Вид сзади

0 с

Як-40 в вихревом следе Ил-76 Рис. 8.28. Зависимость от времени коэффициента подъемной силы самолета Як-40

Рис. 8.29. Зависимости от времени угловых скоростей wx, uy и самолета Як-40

Рис. 8.30. Зависимости от времени коэффициентов моментов крена mx, рыска­ния my и тангажа mz самолета Як-40

 

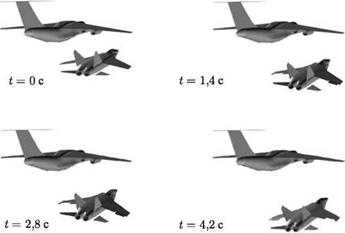
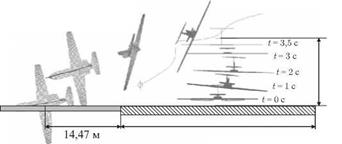
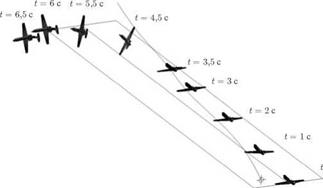
В качестве примера расчета по данному алгоритму на рис. 8.25 и рис. 8.26 показаны траектории движения самолета Як-40, полу­ченные расчетом, в вихревом следе самолета Ил-76, соответству­ющему рис. 4.8, т. е. при катастрофе самолета Як-40 в Ташкенте
16 января 1987 г. Видим, что траектория самолета Як-40 в этом случае повторяет его реальное падение.

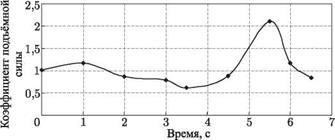
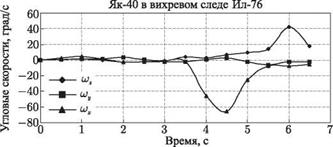
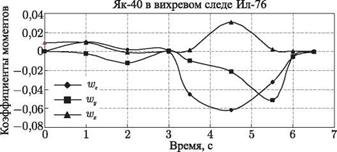
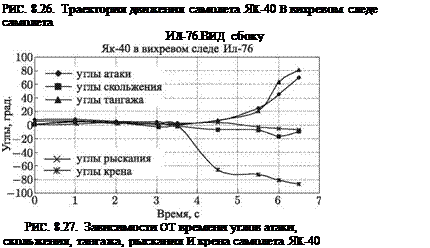
Кроме траектории движения самолета расчетом можно получать другие характеристики. Например, на рис. 8.27 представлены зависи­мости углов атаки, скольжєния, тангажа, рыскания и крена от времени при катастрофе самолета Як-40 (см. рисунки 8.25 и 8.26). Для этого же случая на рис. 8.28 представлена зависимость коэффициента подъ­емной силы от времени, на рис. 8.29 — значения угловых скоростей шх, шу и в зависимости от времени, а на рис. 8.30 — временные зависи­мости коэффициентов моментов крена mx, рыскания ту и тангажа mz. Видно заметное изменение этих коэффициентов на заключительной стадии полета.

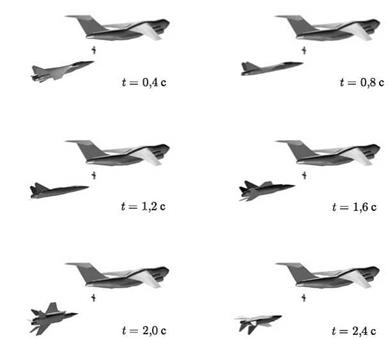
По данной методике можно исследовать характеристики самолетов при их заправке в воздухе. В качестве примера такого исследования на рис. 8.31 представлены взаимные положения самолета-заправщика Ил-78 и заправляемого самолета МиГ-31 в моменты времени поле­та t = 0,4с; 0,8с; 1,2с; 1,6с; 2,0с и 2,4c для случая, когда лет­чик не вмешивается в управление. Заправка происходит от правого крыльевого унифицированного агрегата заправки (УПАЗ). Видим, что

Рис. 8.31. Взаимное положение самолета-заправщика Ил-78 и заправляемого самолета МиГ-31 в различные моменты времени (без летчика)

Рис. 8.32. Взаимное положение самолета-заправщика Ил-78 и заправляемого самолета МиГ-31 в различные моменты времени (с лєтчиком)

под действием вихревого следа заправляемый самолет переворачива­ется на спину. В случае вмешательства летчика самолет сохраня­ет свое нормальное положение в течение всего процесса заправки (рис. 8.32).

1.  

[1] А. С. Гинєвский А. И. Желанников

[2]

где для класса функций H* при p (t) Є H*, t Є [a, b]

P (t) = (t — aP(b _ ty, p (t) Є H на [a, b], 0 < a, y < 1 (4.15)

Покажем, что система (4.14) имеет единственное решение и оно удовлетворяет требуемым граничным условиям. Из физических сооб­ражений первое уравнение системы (4.14) будем рассматривать отно­сительно неограниченной в точке x = —1 функции y (x, t) как сингу­лярное интегральное уравнение на отрезке [—1,1] индекса k = 0.

Разрешая это уравнение относительно y (x, t), получаем